Vanguard Managed Payout Quacks Like a Buffered Withdrawal

The Vanguard Managed Payout Fund (VMP) is a fairly unique offering in the current landscape of mutual funds. While some companies offer funds called “Income Replacement Funds” which are designed to provide an income stream for a fixed period of years, this Vanguard fund is the only fund that I know of that seeks to provide a income stream indefinitely. And the formula used to calculate this income stream has similarities to the buffered withdrawal strategy.
Vanguard’s Managed Payout Formula
The formula used to calculate monthly income for the VMP Fund can be found in the prospectus. Here’s a screenshot of that formula:
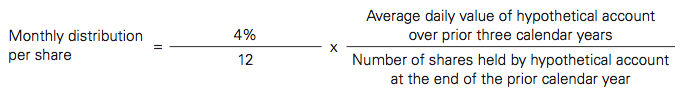
On the left side of the equation, the thing that jumps out is that the income is based on a 4% withdrawal.
The right hand side of the equation describes what value is being multiplied by 4%. Since the overall formula represents the “Monthly distribution per share”, we can estimate the monthly distribution dollar amount by multiplying both sides by the number of shares owned. This means our annual distribution is simply 4% of the average value of the “hypothetical account” over the past 3 years. By reading the prospectus, the “hypothetical account” represents what the account balance would have been if it had been held over the previous 3 years while receiving income according to the above formula.
Graphically, the average of the hypothetical account is taken by averaging the portfolio’s value each day over the past 3 years as illustrated below (I was too lazy to fill in all days of each year so use your imagination).
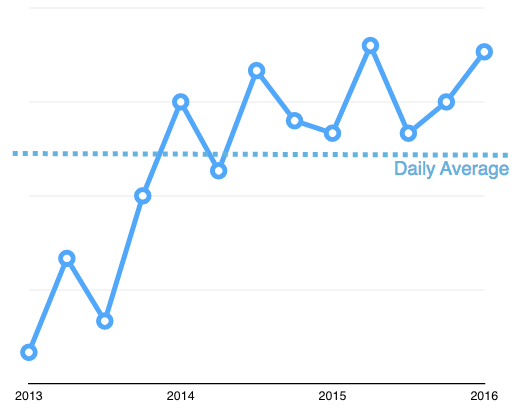
That average is then multiplied by 4% to determine the annual withdrawal amount.
How does this compare to what we do when we take buffered withdrawals from a portfolio?
Buffered Withdrawal
The basic idea of a buffered withdrawal is that, once a year, you take a percentage of your overall portfolio and move that into your spending buffer. Then you divide your spending buffer by your buffer size (in years) to arrive at your income for the coming year. This is illustrated for a 4-year buffer below.
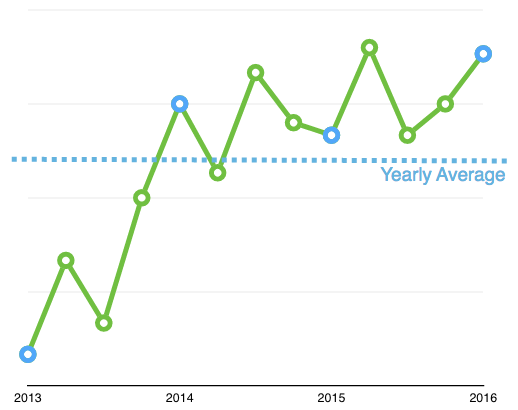
In the illustration, for the buffer calculation at the beginning of 2016, the income would be approximately
income = withdrawal_rate * (V_2013 + V_2014 + V_2015 + V_2016) / 4
Notice that this is 4 years instead of 3 because we are taking the 4 data points at the beginning of each year. This 4-year annual average would be closest in value to the 3-year daily average that VMP uses.
Comparison
The main difference between the VMP formula and the buffered withdrawal formula is the averaging period. The VMP formula averages the account value daily whereas the buffered withdrawal averages once a year. If those averages turn out to be the same then the equations will give the same amount of income. And intuitively, those averages will be pretty close to each other, or at least “close enough” for the purposes of determining how much income to take. The exception would be in years with sharp up or down turns, the daily average could be a bit different than the annual average, but I’m not sure that it would be qualitatively better. In fact, an annual average will be “smoother” because it smooths out the effects of sharp market turns.
I don’t think either method is hugely better than the other. In both cases, if the market is going up, the amount of income to be withdrawn in the next year will go up at a related but smaller rate. Likewise when the market goes down.
Final Thoughts
I found it interesting that the Vanguard Managed Payout formula was pretty similar in theory to the buffered withdrawal strategy. Vanguard doesn’t call it a buffered withdrawal but the effect is the same in that the effects of market swings will be smoothed by averaging the account over recent valuations. If you like the idea of a 4-year buffer that withdrawals at a rate of 4% per year, then the simplicity of the VMP fund might appeal to you. But, if you would like more control over your portfolio, buffer size and withdrawal rate, then you might prefer to follow the withdrawal strategy outlined in the Buffered Withdrawal article.